「ビジネスに使える分析法にはどんなものがあるのだろう?」
「重回帰分析を使ってみたいけど、どうやって計算するのかわからない」
このような悩みをお持ちの方も多いと思います。
私、三木雄信は10年以上前にソフトバンクの孫正義社長の社長室で働き、現在はコーチング英会話トライズ(TORAIZ)を経営しています。孫正義社長の教えを元に、これまでビジネスにおける数値化の重要性や、数値化を行う上で必要な考えかたをご紹介してきました(「【孫社長にたたきこまれたすごい「数値化」仕事術】まとめ」「【トライズでも実践中】数値化仕事術を活用するための7つのポイント」)。
そこで本記事では内容を一歩進めて、著書【孫社長にたたきこまれた すごい「数値化」仕事術】の中から具体的な分析方法を解説していきます。
プロセス分析
ビジネスパーソンなら誰でも、仕事で思うようなアウトプットが出せずに悩むことがあるでしょう。そんな時、「仕事の始点から終点までのどこに問題があるのか」を明らかにし、具体的な改善策を考え出すための手法として、効果抜群なのがプロセス分析です。
プロセス分析とは、その名の通り、仕事の過程をいくつかの段階に分けてとらえることです。例えばマンションの契約では次の図のようにプロセスを策定することができます。

この図では「初回接触・問い合わせ」から「物件案内・内見」までで約半数の顧客が離脱し、「物件案内・内見」から「購入・申し込み」でさらに半数の顧客が離脱していることがわかります。マンションという大きい買い物の場合、後者のステップは平均でも10%程度なので、この結果は飛び抜けて低い購入率というわけではなさそうです。それよりも、前者のステップでの数値は改善の余地があると分かります。
次は前者のステップを改善することを目指します。例えば次のようなルールを決めておくことで、全体のフローを最適化できる可能性があります。
- メールで問い合わせをもらったお客様でも、来店して連絡先を聞いたお客様でも、必ずその日のうちにフォローアップをする。
- 初回の接触から1週間以内に次のアポを取り、物件案内へつなげる。
このような施策を繰り返し、業務の問題点を解消することを心がけましょう。
散布図と単回帰分析
単回帰分析とは1つの変数が、結果にどのような影響を与えるかを1次関数によって表現する分析方法です。
例えば1日の通行量と1ヶ月の契約件数の関係を調べるとします。次の図のように、エクセルに表を作り、横軸に通行量、縦軸に契約件数をとってデータをプロットします。
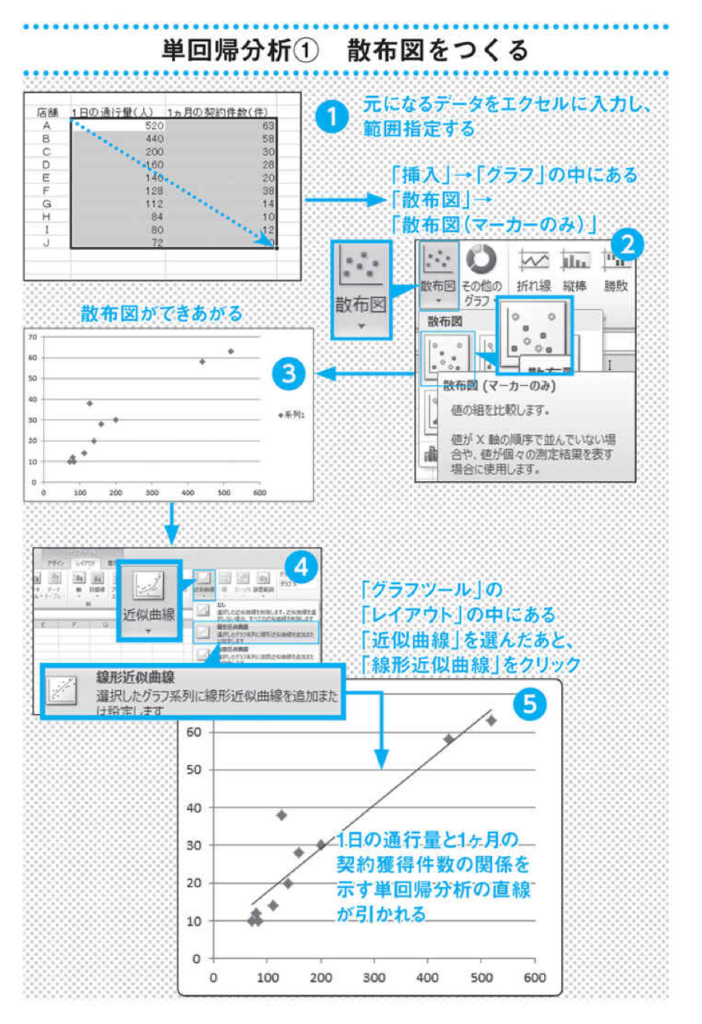
この時に求められる近似曲線が、関数を説明する数式になります。今回の例では「通行量が多ければ多いほど、契約に結びつきやすい」という性質がデータで説明できるようになりました。
重回帰分析
重回帰分析は単回帰分析の応用版といえる分析手法です。どこが異なるかというと、単回帰分析では1つの変数が結果に与える影響を調べることができたのに対し、重回帰分析では複数の変数が結果に与える影響を調べることができるという点です。
具体例として、購入予定のマンションの価格が妥当かどうかを判断するケースを考えてみましょう。ここではマンションの価格に影響を与える可能性のある要素として「階数」「占有面積」「築年数」「バス停までかかる時間」「駅までかかる時間」の5つを仮定します。
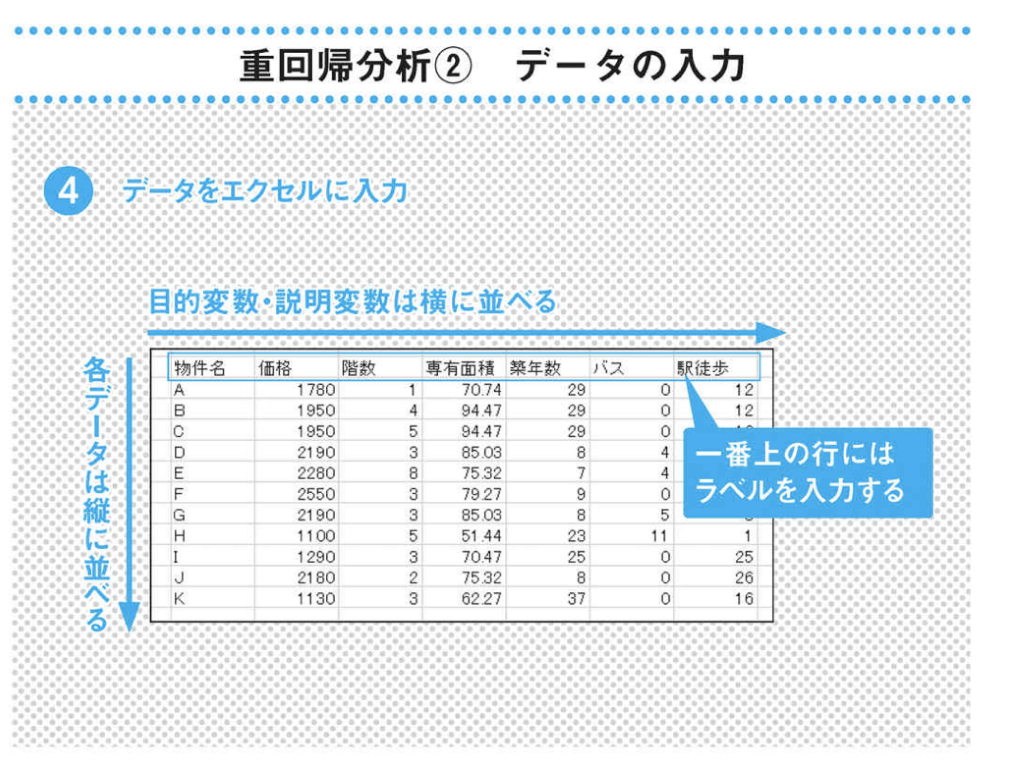
物件AからKまでの11の物件の情報を入力し、データタブから「回帰分析」を選択します。
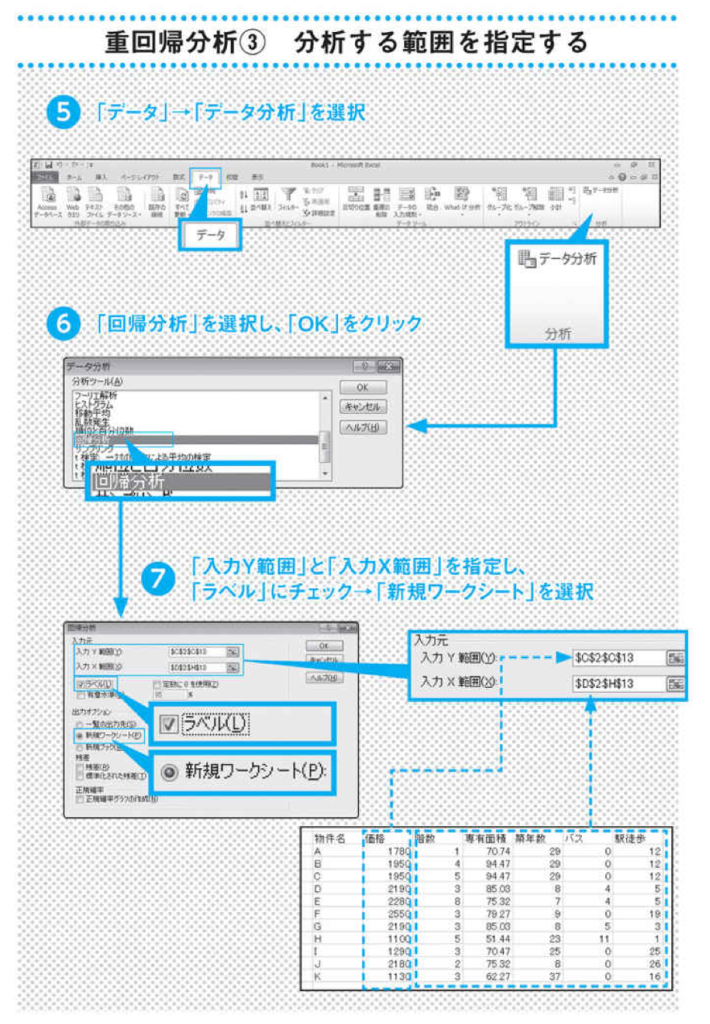
あとはデータの範囲を選択するだけで、統計値を自動的に計算することができます。実用面だけを考えれば、統計値の深い理解もそれほど必要ありません。出力された表の読み方を覚えれば使いこなすことができます。

まず確認するべきは係数です。重回帰分析では次のような関数が出てくるため、
y=(切片)+ax1 + bx2 + cx3 + dx4 + ex5
a, b, c, d, eがそれぞれの要素の係数に該当します。
つまり、今回の表の結果を式に当てはめると、
(マンション価格)=2436 + 3*(階数) + 8*(占有面積)-35*(築年数)-94*(バス停までかかる時間)-24*(駅までかかる時間)
となります。
この式から読み解けることの例としては、
- 築年数が1年古くなるごとに、マンションの価格は35万円安くなる
- バス停までの距離が1分離れるごとに、マンションの価格は94万円安くなる
などが挙げられます。
このように重回帰分析を活用することで、複数の要因が結果に与える影響を定量的に評価することができるようになります。
パレート図分析
パレート図分析とは全体の中である要素が占める割合を視覚化する分析手法です。まずは図の形をイメージするために実例をみてみましょう。
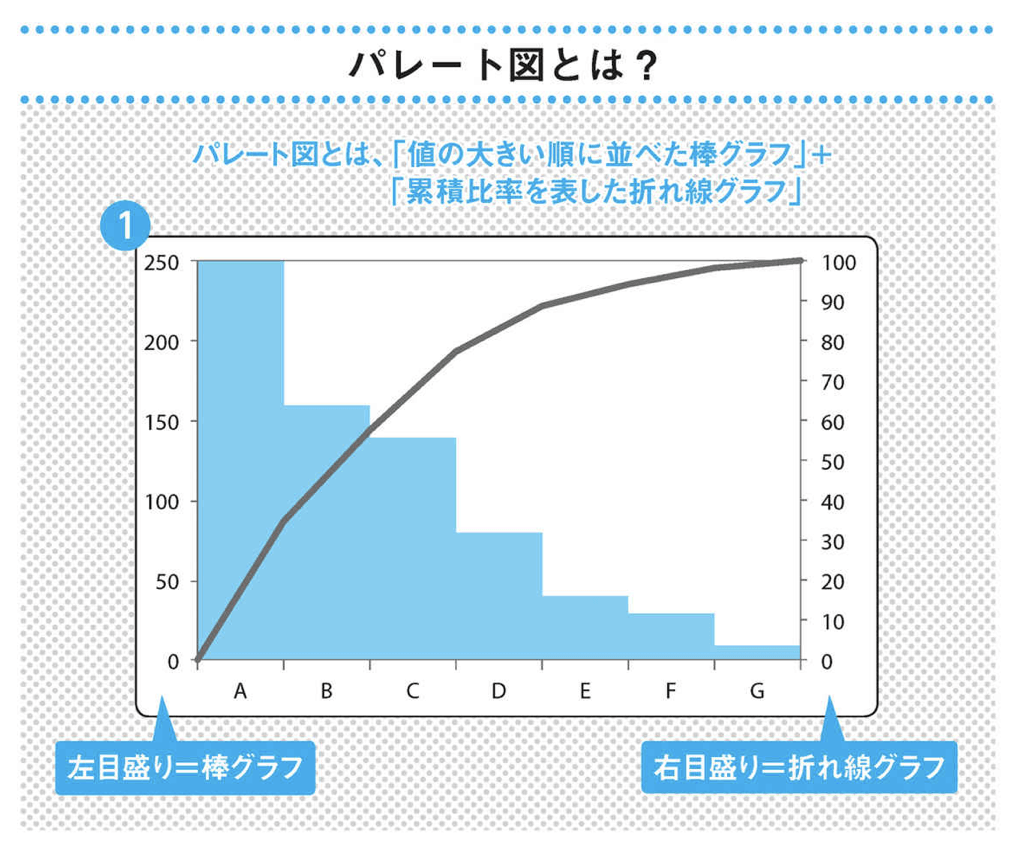
これはあるコールセンターに寄せられた「クレームの種類」と「その割合」を表しています。横軸にはクレームAからGまでの種類をとっています。棒グラフの縦軸はクレームの件数、折れ線グラフの縦軸は全体に占める割合をとっています。
パレート図のメリットはどこまでの問題を解決すれば、全体の何割の問題を解決したことになるかが一目でわかることです。
上記の例では
- Aを解決すれば、全体の4割弱の問題解決になる
- AとBを解決すれば、全体の6割の問題解決になる
- AとBとCを解決すれば、全体の8割の問題解決になる
ということが判別できます。
パレート図は問題と解決策が複数ある際の優先順位づけに活用できるので、無駄な施策を排除して、効果のある施策だけに集中することが可能になります。
T勘定
T勘定は元々、簿記で使われていたスキルです。T字の左側に「収入」、右側に「支出」を書くことで、一目で収支を確認できるという利点があります。(参考資料: https://nishimurazeirishi.com/t-form/)
業務フローの改善で用いられるT勘定では、T字の左側に「入ってきた数」、右側に「出て行った数」を記録して、次の図のように活用します。
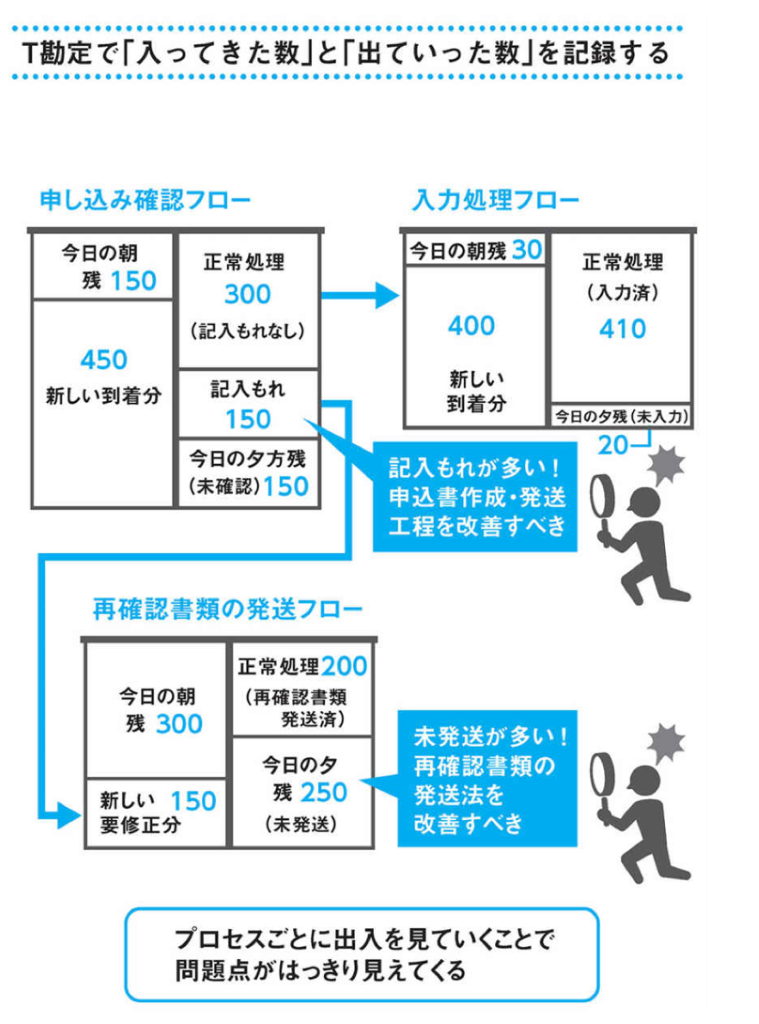
この例では個人型確定拠出年金の申込書を処理する作業を想定しています。届いた申込書の中にはスムーズに処理できるものもあれば、記入漏れがあって再確認書類を発送しなければならないものもあります。そこでどこにボトルネックがあるのかをT勘定で明らかにしようとしています。
まず、T字の左上の数字から、今日の受付開始時点で残っている申込書の数が150部あることがわかります。さらに1日で450部が新たに届きました。T字の右側に目を向けると、そのうち300部を正常に処理でき、150部は記入漏れがあるとわかりました。そして、処理が間に合わずに翌日に持ち越しになる分が150部出たこともわかります。1つ目のT字から、まずは記入漏れを減らすことで、翌日持ち越し分を少なくできることが必要とわかります。
記入漏れがあった書類は、下のT字(再確認書類の発送フロー)へ回ります。こちらでは前日からの持ち越し分が300部、当日に発生したのが150部あると分かります。そのうち、200部は正常に処理でき、250部は処理が間に合わずに残ってしまいました。ここで処理が間に合っていない部数が多いこともボトルネックと考えられるので、「再発送書類の発想法を見直すべき」とわかります。
このようにT勘定は複雑な出入りの伴う流れを模式化し、どこに問題があるかをあぶり出すことに活用できます。
差異分析
差異分析とは「計画」と「実績」を比較し、差異が生じた原因を分析する手法です。具体的な例を見ていきましょう。あるマーケティングチームでは、自社がリリースした新サービスの認知度を上げるため、インターネットで広告キャンペーンを展開しました。ところが実際にやってみると、当初の予算よりも金額がオーバーしていました。当初想定していた予算は次の通りでした。
- クリック単価:100円
- クリック数::1万回
しかし、実際の数字は次のようになりました。
- クリック単価: 120円
- クリック数::1万2000回
それではクリック単価が20円上がったことと、クリック数が2000回上がったことのどちらが予算オーバーの主な原因になっているのでしょうか?
この問いを明らかにするために、横軸にクリック数、縦軸にクリック単価をとったグラフを考えてみます。
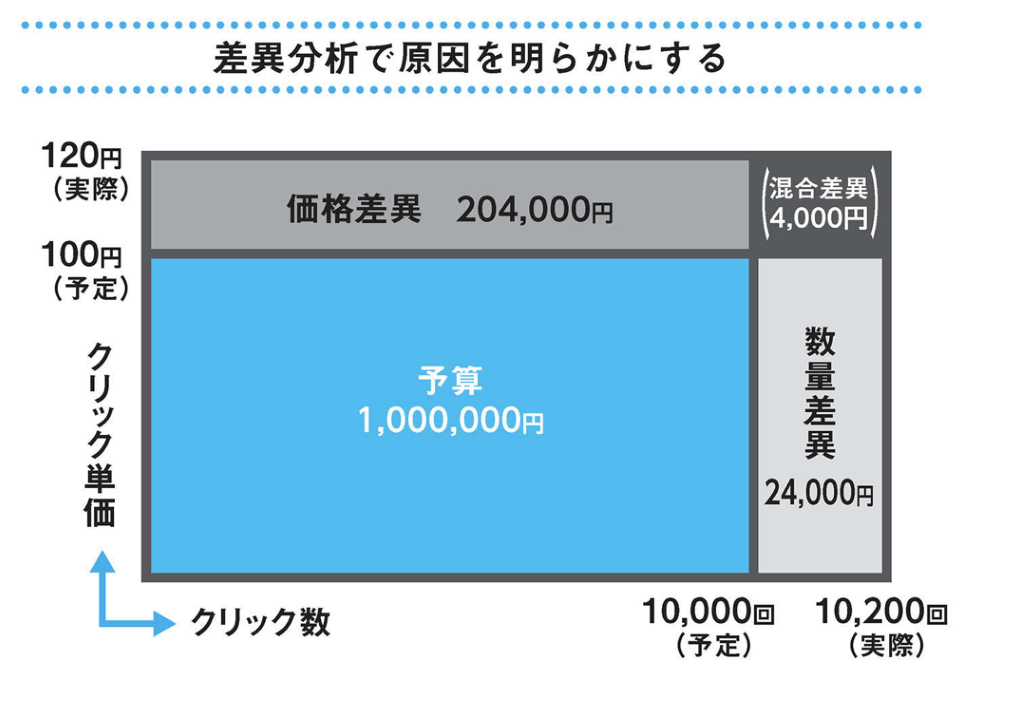
するとクリック単価の上昇による差異(価格差異)が20万4000円、クリック数の増加による差異(数量差異)が2万4000円あることがわかります。つまり、クリック単価の上昇が、予算オーバーの主な原因であったと断定できます。
このようにして「計画」と「実績」のギャップを分析すれば、何から優先しえ手を打つべきかが明らかになります。
LTV分析
LTVとは顧客が一生に間に生み出す利益を指す「Life Time Value」の頭文字をとった用語です。一般にお客さんはキャンペーンを行うと退会を踏みとどまり、幾らかのお金を消費してくれます。しかしキャンペーンを行うにも費用がかかるので、何段階のキャンペーンを打つべきかを決める必要があります。そこで活用できるのがLTV分析です。
具体的な例を用いて説明しましょう。あるアプリの広告宣伝費にいくらの予算をかけるべきかを決めるために、キャンペーンAからHの運用試験を小規模で行い、次のような結果を得ました。
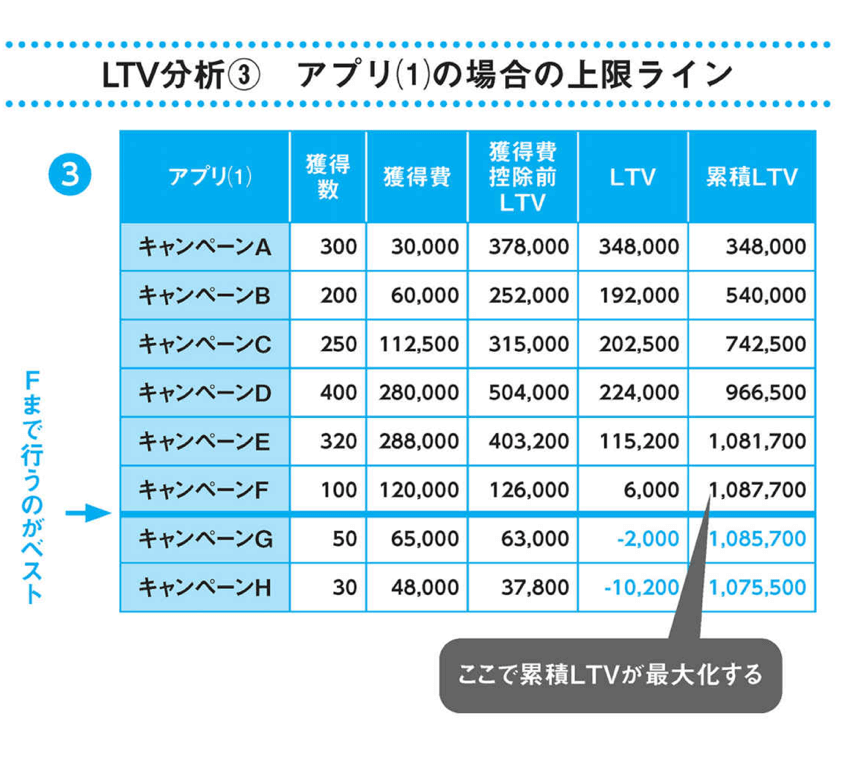
獲得数は「入会したユーザーの数」、獲得費は「キャンペーン費用」、獲得費控除前LTVは「獲得したユーザーが生み出した利益」、LTVは「獲得したユーザーが生み出した利益から、キャンペーン費用を差し引いたもの(純利益)」、累積LTVは「キャンペーンAから順に行っていった際の純利益」を表しています。
すると、キャンペーンFまでは累積LTVが増加し、キャンペーンG, Hへ進むと累積LTVが減少することが明らかになります。したがって、今回の例では「キャンペーンFまで行うのが最適」と根拠を持って示せることが分かります。
まとめ
漠然と数値を眺めるのではなく、適切に数値を分けて、種々の分析手法に乗せることで、改善に必要な傾向が見えてきます。実際に、私も数値化仕事術を実践することによって、コーチング英会話トライズ(TORAIZ)の経営をあっという間に軌道に乗せることに成功しました。より詳しい情報を著書【孫社長にたたきこまれた すごい「数値化」仕事術】で公開していますので合わせてご参照ください。










